Moving forward isn't the only kind of kinetic energy; it also takes energy to spin the wheels. The rotational kinetic energy of the wheels is given by
 .
.
where I is the moment of inertia and ω is the angular velocity. The angular velocity is related to the linear velocity through
Where r is the radius of the wheel. The moment of inertia for a ring of radius r and mass m' is
and for a disk, it is
For a Pinewood Derby wheel, the moment of inertia can be approximated by[1]
 .
.
The rotational kinetic energy for the four wheel is therefore
 .
.
This turns out to be 0.094 J of energy stored in the four wheels at the car's top speed of 4.75 m/s (see the table below). Compare that to the 1.7 J gravitational potential energy from above. Almost 6 % of that energy is stored in the spinning wheels and about 94 % is available for the car's forward velocity.
The potential energy relation is now
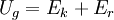 ,
,
and solving for the velocity
for a car of mass m with wheels of mass m'. Now it is clear why the heaviest possible car is the fastest: for large m, the denominator approaches 1 and the velocity is the same as the above case for the frictionless block: 4.9 m/s. With standard 3.6 g wheels, a 141.7 g (5 ounce) car has a velocity of 4.75 m/s at the bottom of the track. A 113.4 g (4 ounce) car has a velocity of 4.72 m/s.
The advantage of light wheels is also clear. The slowest car is one with the most mass in the wheels. If m' = m (four 35 g wheels rolling down the track!) the velocity is 2.7 m/s. With 3.6 g wheels, the velocity is 4.75 m/s; with 1 g light wheels, the velocity is 4.85 m/s. Another way to look at it is that a light wheel car has less than 2 % of its kinetic energy in the wheels while the standard wheel car has almost 6 %.
Raising one wheel reduces the rotational energy as long as that wheel doesn't touch the ground. The velocity of a three wheel (3.6 g) car is 4.78 m/s, while a raised light wheel car can reach 4.86 m/s.



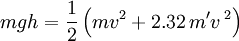

No comments:
Post a Comment