Potential and kinetic energy

____We'll start out with the simplest possible case and then add more complexity to get more accuracy. First we consider a 141.7 gram (5 ounce) frictionless block sliding down an 8.53 m (28 foot) track where the car starts 1.219 m (4 feet) above the finish line. The energy that makes a pinewood derby car roll down the ramp is potential energy (symbol U_g). At the bottom of the ramp, this energy is converted into kinetic energy (symbol E_k).

The potential energy can be calculated using the formula

.

where m is the mass of the car, g is the acceleration due to gravity (9.807 m/s² = 32.17 ft/s² at the earth's surface) and h is the height of the car on the starting ramp (about 4 feet = 1.22 meters). The potential energy stored in a 5 ounce pinewood derby car is about 1.7 kg m²/s²= 1.7 J. The quantity 1.7 joule of energy is the same as 1.7 watts of power applied for one second.

The kinetic energy can be calculated using the formula

.

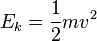where v is the velocity (speed) of the car, measured in meters per second (in SI units). If all of the potential energy is converted into kinetic energy, then

and, substituting from above,

since the mass is on both sides of the equation, you can divide both sides by m and cancel (remove) the mass from the equation.

and, rearranging, the velocity is found from

___The velocity doesn't depend on the mass, just as Galileo demonstrated at the Leaning Tower of Pisa and, during the Apollo 15 landing, David Scott demonstrated on the moon. The velocity of any object falling from a height of 1.219 m is 4.890 m/s (11 MPH).

How fast does the block travel down the track? The fastest trip to the ground is straight down and the time to fall is the distance divided by the average speed, which is half of the final speed:

.

The car takes 0.499 s to fall straight to the ground.

Now consider an 8.53 m (28 foot) track that consists of a 30° ramp followed by a flat portion to the finish. The ramp section is 2.43 m (8 feet) long and the flat section is 6.1 m (20 feet) long. The car travels the 2.43 m ramp at an average velocity of v / 2 = 2.445 m/s and then travels the remaining 6.1 m at 4.890 m/s. The total time is

.

The block takes 0.992 s to go down the ramp and 1.245 s on the flat for a total of 2.237 s. The mass doesn't affect the speed - a frictionless feather is as fast as a lead brick.