An idealized track

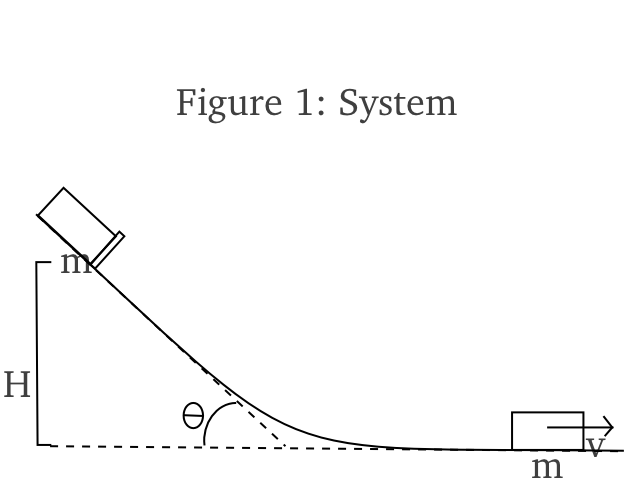
__Now that we know how fast an idealized car can go, let's let it run down an idealized track. A typical pinewood derby track is 32 feet long with 4 feet for the starting gate and arresting gear, leaving 8.534 m for travel. The first part of the track has a slope of about 20°, a curved transition section, followed by a flat section to the finish. The track can be approximated by a straight ramp section with length $d 1$ followed by a flat section with length $d 2$ . Times calculated using the straight track approximation differ by less than 0.001 s compared to those obtained using a curved track and numerical integration.^[2] With the straight track and 20° slope, $d 1$ = 3.564 m and $d 2$ = 4.970 m. The car travels down the sloped section $d 1$ starting at zero velocity and accelerating to a velocity $v\,$ with an average speed of $v/2\,$ . 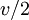It then travels the distance $d 2$ at a velocity $v\,$ . The total time is then

$t= 2\frac{d_1}{v} + \frac{d_2}{v}$

or 12.098/v seconds, if the velocity is specified in meters per second. Run times under different conditions are given in the table below.

Conditions	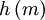$h\,(m)$	$m\,(g)$	$m'\,(g)$	$v\,(m/s)$	$t\,(s)$
Frictionless Block	1.219	any	0	4.89	2.47
Stock Wheels	1.219	141.7	3.6	4.75	2.55
Light (4 oz) Car	1.219	113.4	3.6	4.72	2.56
Light Wheels	1.219	141.7	1.0	4.85	2.49
One Raised Wheel	1.219	141.7	2.7	4.78	2.53
Light Wheels, One Raised	1.219	141.7	0.75	4.86	2.49
Rear Bias (Stock Wheels)	1.243	141.7	3.6	4.80	2.52

Center of Mass

__Up to this point, we have approximated the car as a point mass that starts 1.219 m above the finish and winds up at 0 m. As anyone familiar with pinewood derby knows, it is usually best to keep the center of mass as far back as possible, in part to increase the gravitational potential energy. How much faster is a car with the center of mass shifted to the back? Consider two cars, Car A with the center of mass at the center of the block and Car B with the center of mass 25.4 mm (one inch) in front of the rear axle in an extended wheelbase configuration with the axle 15.9 mm (5/8") from the rear of the block. The center of mass of the Car B is 47.6 mm behind Car A and 23.8 mm higher on a 30° slope. Car A starts at 1.219 m and (as shown above) has a maximum velocity of 4.75 m/s and 2.55 s time; Car B starts at 1.243 m and has a maximum velocity of 4.80 m/s and a 2.52 s time.

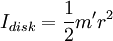
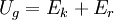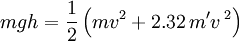
Rotational kinetic energy

Moving forward isn't the only kind of kinetic energy; it also takes energy to spin the wheels. The rotational kinetic energy of the wheels is given by

$E_r = \frac{1}{2}I\omega^2$ .

where I is the moment of inertia and ω is the angular velocity. The angular velocity is related to the linear velocity through

$\omega = r\,v$

Where $r$ is the radius of the wheel. The moment of inertia for a ring of radius r and mass $m'$ is

$I_{ring} = m'r^2\,$

and for a disk, it is

$I_{disk} = \frac{1}{2}m'r^2\,$

For a Pinewood Derby wheel, the moment of inertia can be approximated by^[1]

$I_{wheel} = 0.58\,m'r^2\,$ .

The rotational kinetic energy for the four wheel is therefore

$E_{r} = 4 \times 0.58\,m'\omega^2r^2 = \frac{1}{2} (2.32\,m')v\,^2\,$ .

This turns out to be 0.094 J of energy stored in the four wheels at the car's top speed of 4.75 m/s (see the table below). Compare that to the 1.7 J gravitational potential energy from above. Almost 6 % of that energy is stored in the spinning wheels and about 94 % is available for the car's forward velocity.

The potential energy relation is now

$U_g = E_k + E_r\,$ ,

$m g h = \frac{1}{2} \left( mv^2 + 2.32\,m'v\,^2 \right)\,$

and solving for the velocity

$v = \sqrt {\cfrac {2gh} {1 + 2.32 \cfrac {m'}{m} } } \,$

for a car of mass m with wheels of mass $m'$ . Now it is clear why the heaviest possible car is the fastest: for large m, the denominator approaches 1 and the velocity is the same as the above case for the frictionless block: 4.9 m/s. With standard 3.6 g wheels, a 141.7 g (5 ounce) car has a velocity of 4.75 m/s at the bottom of the track. A 113.4 g (4 ounce) car has a velocity of 4.72 m/s.

The advantage of light wheels is also clear. The slowest car is one with the most mass in the wheels. If $m' = m$ (four 35 g wheels rolling down the track!) the velocity is 2.7 m/s. With 3.6 g wheels, the velocity is 4.75 m/s; with 1 g light wheels, the velocity is 4.85 m/s. Another way to look at it is that a light wheel car has less than 2 % of its kinetic energy in the wheels while the standard wheel car has almost 6 %.

Raising one wheel reduces the rotational energy as long as that wheel doesn't touch the ground. The velocity of a three wheel (3.6 g) car is 4.78 m/s, while a raised light wheel car can reach 4.86 m/s.

Potential and kinetic energy

____We'll start out with the simplest possible case and then add more complexity to get more accuracy. First we consider a 141.7 gram (5 ounce) frictionless block sliding down an 8.53 m (28 foot) track where the car starts 1.219 m (4 feet) above the finish line. The energy that makes a pinewood derby car roll down the ramp is potential energy (symbol $U g$ ). At the bottom of the ramp, this energy is converted into kinetic energy (symbol $E k$ ).

The potential energy can be calculated using the formula

$U_g = m g h \,$ .

where m is the mass of the car, $g$ is the acceleration due to gravity (9.807 m/s² = 32.17 ft/s² at the earth's surface) and h is the height of the car on the starting ramp (about 4 feet = 1.22 meters). The potential energy stored in a 5 ounce pinewood derby car is about 1.7 kg m²/s²= 1.7 J. The quantity 1.7 joule of energy is the same as 1.7 watts of power applied for one second.

The kinetic energy can be calculated using the formula

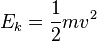$E_k = \frac{1}{2}mv^2$ .

where v is the velocity (speed) of the car, measured in meters per second (in SI units). If all of the potential energy is converted into kinetic energy, then

$U_g = E_k \,$

and, substituting from above,

$m g h = \frac{1}{2}mv^2 \,$

since the mass is on both sides of the equation, you can divide both sides by $m$ and cancel (remove) the mass from the equation.

$g h = \frac{1}{2}v^2 \,$

and, rearranging, the velocity is found from

$v = \sqrt{2 g h} \,$
___The velocity doesn't depend on the mass, just as Galileo demonstrated at the Leaning Tower of Pisa and, during the Apollo 15 landing, David Scott demonstrated on the moon. The velocity of any object falling from a height of 1.219 m is 4.890 m/s (11 MPH).: How fast does the block travel down the track? The fastest trip to the ground is straight down and the time to fall is the distance divided by the average speed, which is half of the final speed:; $t = \frac{d}{v/2}\,$ .

The car takes 0.499 s to fall straight to the ground.

Now consider an 8.53 m (28 foot) track that consists of a 30° ramp followed by a flat portion to the finish. The ramp section is 2.43 m (8 feet) long and the flat section is 6.1 m (20 feet) long. The car travels the 2.43 m ramp at an average velocity of $v / 2 =$ 2.445 m/s and then travels the remaining 6.1 m at 4.890 m/s. The total time is

$t_{total} = t_{ramp} + t_{flat}\,$ .

The block takes 0.992 s to go down the ramp and 1.245 s on the flat for a total of 2.237 s. The mass doesn't affect the speed - a frictionless feather is as fast as a lead brick.

The physics of the pinewood derby

The Physics of the Pinewood Derby

Every year, most Cub Scout packs in the United States hold a contest they call the Pinewood Derby. Before the event, each scout and an adult helper craft a car out of a block of wood that will compete in a series of races during the event.

The race course is a sloped wooden ramp. At the top of the ramp is a wooden drawbridge that starts in the up position. Each car is placed above the drawbridge in its own lane so that the front of the car rolls to a rest touching the drawbridge. The race is started by releasing the drawbridge, letting it fall to the open position. The cars roll down the ramp. The first to reach the finish line at the bottom is the winner.

I last competed in a Pinewood Derby race some 14 years ago. My dad who helped me build the car had an electrical engineering background, and since then, I have followed in his engineering footsteps. We thought at the time that we had a marked advantage on our competitors since we theoretically knew more about how to build the car correctly. Sadly, while we did better than average in our races, we never did exceptionally.

For many years, I have wondered why our cars never performed better. Our cars were designed to be aerodynamic, in fact little more than skateboards. They tipped the weight scales at just under the allowable limit. We sanded the burrs out of the wheel wells, and added lubrication for even less friction. Still, it seemed that there was something that we missed.

One night recently, as I was lying in bed trying to fall asleep, it came to me! The more I thought about it, the more I thought I realized that I should have seen the answer much sooner. The answer lies in weight distribution.

Warning:Here comes some heavy-duty physics.

Consider the following diagram of the system:

H is the height of the drawbridge.
m is the mass of the car.
v is the velocity of the car once it reaches the bottom of the ramp.
x is the distance along the length of the car from the front of the car to the car's center of mass.
y is the distance along the height of the car from the bottom of the car to the car's center of mass.

The initial energy of the car is its potential energy relative to the end of the track.

Eo = mg(H + x sin(theta) + y cos(theta));

The end energy of the car is equal to its potential energy relative to the end of the track, plus it's kinetic energy.

Ef = mgy + 0.5 mv^2

The initial energy of the system equals the final energy of the system:

Eo = Ef

mg(H + x sin(theta) + y cos(theta)) = mgy + 1/2 mv^2

mg(H + x sin(theta) - y (1-cos(theta))) = 1/2 mv^2

v = (2g(H + x sin(theta) - y (1 - cos(theta))))^1/2

We have now solved for the final velocity of the car based on the properties of the ramp, and the properties of the car. It is important to note that this equation does not depend on the mass of the car, but it does depend on the location of the center of mass of the car relative to the dimensions of the car.

Given that the physical properties of the ramp, such as it's height and angle of inclination, are the same for all cars in the race, there is no advantage to be gained by altering the ramp (never mind the fact that the pack leader would never allow it). This leaves us to consider the changes we can make in our own car, that is, the location of the center of mass.

Our equation can be simplified by writing it as:
v = (C0 + C1 * x - C2 * y)^1/2
where:
C0 = 2gH
C1 = 2g sin(theta)
C2 = 2g (1 - cos(theta))

If we look at this equation, we can see that v gets larger as x gets larger, but that v gets smaller as y gets larger. The place in the car where the x is large and the y is small is the bottom back corner of the car.

Bottom line: Centering the weight of your car as much as possible toward the bottom, back corner of your car will make it faster during the race.

Now, I know a lot of folks out there are somewhat skeptical of this whole math and physics thing. I would like to point out this page, written by a young boy scout for a science fair project, where he does an experiment that shows empyrically that having the center of mass in the back of the car produces faster cars. Good luck building.

How to make speed pinewood derby car

Google

Labels

Followers

Blog Archive

About Me

Thursday, February 4, 2010